Model Penemuan Terbimbing dalam Pembelajaran Matematika
Model Penemuan Terbimbing dalam Pembelajaran Matematika - Sebelum membahas Model Penemuan Terbimbing, ada baiknya terlebih dahulu kita tinjau sejenak Model Penemuan Murni. Dalam Model Penemuan Murni, yang oleh Maier (1995: 8) disebutnya sebagai “heuristik“, apa yang hendak ditemukan, jalan atau proses semata-mata ditentukan oleh siswa itu sendiri. Menurut Jerome Bruner (Cooney, Davis: 1975: 138), penemuan adalah suatu proses, suatu jalan/cara dalam mendekati permasalahan bukannya suatu produk atau item pengetahuan tertentu. Proses penemuan dapat menjadi kemampuan umum melalui latihan pemecahan masalah dan praktek membentuk dan menguji hipotesis. Di dalam pandangan Bruner, belajar dengan penemuan adalah belajar untuk menemukan, dimana seorang siswa dihadapkan dengan suatu masalah atau situasi yang tampaknya ganjil sehingga siswa dapat mencari jalan pemecahan.
Baca juga : Teori Belajar Mengajar Menurut Jerome S. Bruner
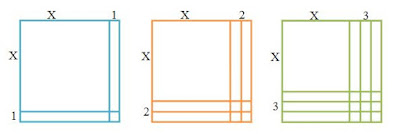
Sebagai ilustrasi bagaimana Bruner menerangkan dengan contoh suatu pelajaran penemuan dapat ditemukan di dalam bukunya Toward a Theory of Instruction (1966: 59-68). Ilustrasi tersebut menunjukkan bagaimana seorang siswa dihadapkan dengan suatu persegi dengan ukuran x dan persegi-persegi satuan. Siswa harus membangun persegi dengan sebanyak potongan persegi-persegi satuan yang diperlukan. Para siswa diharapkan dapat menduga suatu kesimpulan mengenai binomial serta melihat hubungannya dengan melihat potongan persegi dengan ukuran x dan persegi satuan seperti pada gambar berikut ini:
Dalam kegiatan pembelajarannya, siswa diarahkan untuk menemukan sesuatu, merumuskan suatu hipotesa, atau menarik suatu kesimpulan sendiri. Kadang-kadang model penemuan ini memerlukan waktu lebih lama untuk seluruh kelas atau kelompok kecil siswa dalam menemukan suatu obyek matematika dari pada menyajikan obyek tersebut kepada mereka.
Metode Penemuan Murni ini kurang tepat karena pada umumnya sebagian besar siswa masih membutuhkan konsep dasar untuk dapat menemukan sesuatu. Hal ini terkait erat dengan karakteristik pelajaran matematika yang lebih merupakan deductive reasoning dalam perumusannya. Di samping itu, penemuan tanpa bimbingan dapat memakan waktu berhari-hari dalam pelaksanaannya atau bahkan siswa tidak berbuat apa-apa karena tidak tahu, begitu pula jalannya penemuan. Jelas bahwa model penemuan ini kurang tepat untuk siswa sekolah dasar maupun lanjutan apabila tidak dengan bimbingan guru, karena materi matematika yang ada dalam kurikulum tidak banyak yang dapat dipelajari karena kekurangan waktu bahkan siswa cenderung tergesa-gesa menarik kesimpulan dan tidak semua siswa dapat menemukan sendiri. Mengingat hal tersebut timbul metoda pembelajaran dengan penemuan yang dipandu oleh guru.
Implementasi Model Penemuan Terbimbing
Metode penemuan yang dipandu oleh guru ini pertama dikenalkan oleh Plato (Baca juga: Biografi Plato Tokoh Elit Pemikiran Barat) dalam suatu dialog antara Socrates dan seorang anak, maka sering disebut juga dengan metoda Socratic (Cooney, Davis: 1975, 136). Metode ini melibatkan suatu dialog/interaksi antara siswa dan guru di mana siswa mencari kesimpulan yang diinginkan melalui suatu urutan pertanyaan yang diatur oleh guru. Salah satu buku yang pertama menggunakan teknik penemuan terbimbing adalah tentang aritmetika oleh Warren Colburn yang pelajaran pertamanya berjudul: Intellectual Arithmetic upon the Inductive Method of Instruction, diterbitkan pada tahun 1821, yang isinya menekankan penggunaan suatu urutan pertanyaan dalam mengembangkan konsep dan prinsip matematika. Ini menirukan metode Socratic di mana Socrates dengan pertolongan pertanyaan yang ia tanyakan dimungkinkan siswa untuk menjawab pertanyaan tersebut.
Dialog di bawah ini menerangkan contoh strategi untuk membimbing siswa dalam menyimpulkan bahwa a pangkat 0 = 1. Pertanyaan yang tepat dari seorang guru akan sangat membantu siswa. Contoh dialog antara guru dan siswa adalah sebagai berikut:
Interaksi dalam metode ini menekankan pada adanya interaksi dalam kegiatan belajar mengajar. Interaksi tersebut dapat juga terjadi antara siswa dengan siswa (S – S), siswa dengan bahan ajar (S – B), siswa dengan guru (S – G), siswa dengan bahan ajar dan siswa (S – B – S) dan siswa dengan bahan ajar dan guru (S – B – G). Interaksi yang mungkin terjadi tersebut dapat digambarkan sebagai berikut:
Interaksi dapat pula dilakukan antara siswa baik dalam kelompok-kelompok kecil maupun kelompok besar (kelas). Dalam melakukan aktivitas atau penemuan dalam kelompok- kelompok kecil, siswa berinteraksi satu dengan yang lain. Interaksi ini dapat berupa saling sharing atau siswa yang lemah bertanya dan dijelaskan oleh siswa yang lebih pandai. Kondisi semacam ini selain akan berpengaruh pada penguasaan siswa terhadap materi matematika, juga akan dapat meningkatkan social skills siswa, sehingga interaksi merupakan aspek penting dalam pembelajaran matematika. Menurut Burscheid dan Struve (Voigt, 1996:23), belajar konsep-konsep teoritis di sekolah, tidak cukup hanya dengan memfokuskan pada individu siswa yang akan menemukan konsep-konsep, tetapi perlu adanya social impuls di sekolah sehingga siswa dapat mengkonstruksikan konsep-konsep teoritis seperti yang diinginkan.
Interaksi dapat terjadi antar guru dengan siswa tertentu, dengan beberapa siswa, atau serentak dengan semua siswa dalam kelas. Tujuannya untuk saling mempengaruhi berpikir masing-masing, guru memancing berpikir siswa yaitu dengan pertanyaan-pertanyaan terfokus sehingga dapat memungkinkan siswa untuk memahami dan mengkontruksikan konsep-konsep tertentu, membangun aturan-aturan dan belajar menemukan sesuatu untuk memecahkan masalah.
Demikianlah uraian singkat mengenai Model Penemuan Terbimbing dalam Pembelajaran Matematika. Semoga dapat bermanfaat dan menambah khazanah keilmuan teman-teman.



Terima kasih telah berkomentar dengan baik dan sopan.
EmoticonEmoticon